Choose the faster library, OpenBLAS or MKL for AMD CPUs.
Introduction
When it comes to scientific computing or matrix operations, BLAS (basic linear algebra subprograms) and LAPACK (linear algebra package) are the core libraries that provides basic algorithms. Additionally, there exist many alternative and more powerful libraries (OpenBLAS ), Intel Math Kernle Library (MKL) , AMD Optimizing CPU Libraries (AOCL) , etc) that can speed the matrix operations.
The MKL is one of the most famous algebra libraries, which is indeed becoming the actual standard. However, it is said that MKL is only optimized for Intel CPUs and performs poorly on AMD CPUs. OpenBLAS and AOCL are preferred for AMD CPUs. While some discussions (reddit , report ) also show that the newer versions of MKL perform similarly as OpenBLAS on AMD CPUs.
To choose the proper library, I made a simple performance test based on Python Numpy. Remember that the test is not strict nor comprehensive at all. Those who want to choose the proper one should make a benchmark test on your own platform, especially for your specific purposes.
Test
1. Platform
- My laptop was used for the test. It has the AMD RYZEN 5800H CPU (8 CPU cores and 16 threads, TDP 45W) and 32G memory.
- The OS were Window 10 and WSL1 (Ubuntu 20.04).
- Python and numpy version:
| Environment | OS | Python version | Library |
|---|---|---|---|
| Env1 | Win10 | 3.6 | MKL 2020.2 |
| Env2 | WSL1 | 3.9 | MKL 2021.2 |
| Env3 | WSL1 | 3.9 | OpenBLAS |
- To install the MKL based numpy, simply run
conda install numpy - To install the OpenBLAS based numpy, simply run
pip install numpy - After installation, use
numpy.show_config()to check whether the numpy library was properly configured.
2. Test code
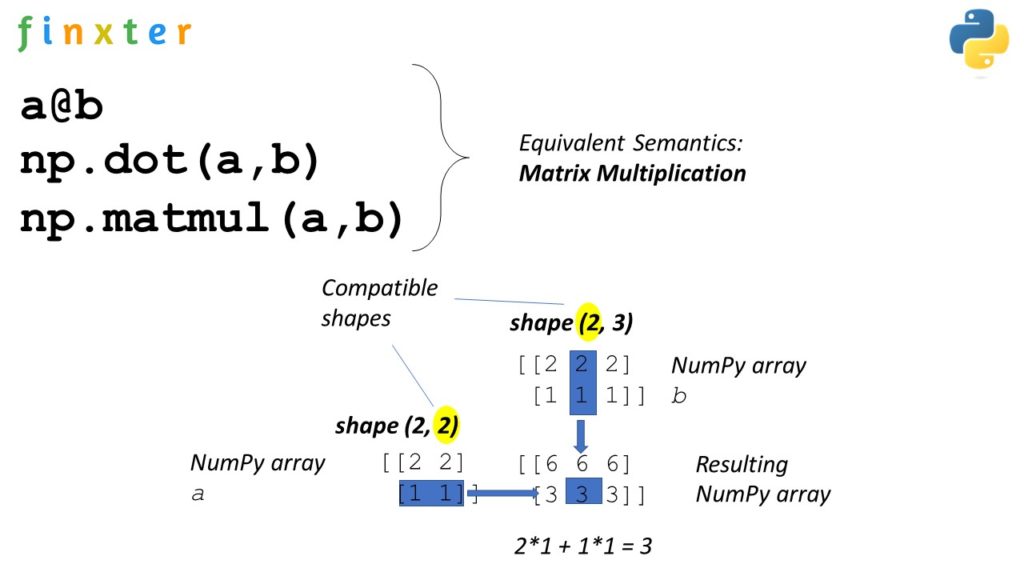
I tried a very simple test code, which only covered matrix multiplication and eigenvalue decomposition.
import numpy as np
size = 1000
a = np.random.randn(size, size)
b = np.random.randn(size, size)
%timeit (np.dot(a,b))
%timeit (np.linalg.eig(a))
- The
sizeparameter was set to 1000, 4000, and 10000, respectively. %timeitis a magic function used on the Jupyter notebooks (IPython).
3. Performance comparison
| size | Matrix Multiplication | EigValue Decomposition | |
|---|---|---|---|
| Env1 | 1000 | 17ms | 600ms |
| 4000 | 700ms | 21.5s | |
| 10000 | 10.3s | Too long to test | |
| Env2 | 1000 | 14.2ms | 586ms |
| 4000 | 609ms | 21.9s | |
| 10000 | 11.4s | Too long to test | |
| Env3 | 1000 | 10.1ms | 738ms |
| 4000 | 614ms | 26.4s | |
| 10000 | 8.24s | Too long to test |
From the table above, we can conclude that
- Using OpenBLAS, the matrix multiplication is faster than using MKL.
- Using OpenBLAS, the eigenvalue decomposition is slower than using MKL.
- The performance differences are not significant and we should choose the proper library based on the specific projects (whether containing many multiplication or decomposition operations).
- I also tried the
mkl_serv_intel_cpu_trueto force to use best performing routines. However, it turned out that the results before and aftermkl_serv_intel_cpu_trueare no different.
Another point is when using OpenBLAS, the CPU usage was nearly 80%, but only around 50% when using MKL. That might be because MKL could not make full use of the AMD CPUs.
Conclusion
Using OpenBLAS makes matrix multiplication faster, but makes eigenvalues decomposition slower. The performance differences are not significant.
In my own opinion, the newer version MKL provides more functions, and similar performance, which makes it suitable for AMD CPUs.
Next, I will try to compare more software based on MKL and OpenBLAS, such as Eigen, Armadillo, and so on.